Парадокс шеста и сарая. (из книги Парадокс. Девять великих загадок физики. Профессор Джим Аль-Халили)
— Чему равна длинна шеста?
— Зависит от того, как быстро он движется…
С большой вероятностью вы никогда раньше не слышали об этом парадоксе, если только не учились на физическом факультете. Это один из известных примеров, встречающихся в учебниках физики в разделах, которые посвящены теории относительности Эйнштейна и подчеркивают некоторые особенности расчетов, касающихся природы пространства и времени.
Прыгун с шестом бежит, удерживая шесть параллельно земле, на очень высокой скорости. Настолько высокой, что она близка к скорости света! Он приближается к сараю, длина которого равна длине шеста. Ему известно об этом, потому что перед забегом он сравнил длину шеста с длиной сарая. Передняя и задняя двери сарая открыты настежь, и он пробегает через него, не замедляя ход. Ничего не зная о теории относительности, мы предположим, что в определенный момент времени задняя часть шеста только-только войдет в сарай, а передняя в тот же самый момент выйдет из него.
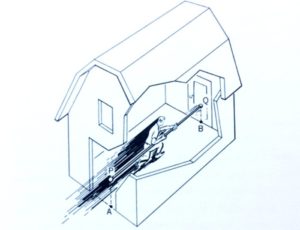Все так бы и было, если бы спортсмен бежал с нормальной человеческой скоростью. Но нет, он бежит на околосветной скорости, а именно при таких скоростях начинают проявляться всевозможные странные и удивительные физические эффекты, предсказанные теорией относительности Эйнштейна. Один из них, имеющий центральное значение для этого случая, заключается в том, что объект, движущийся с очень большой скоростью, становится короче, чем он был в состоянии покоя. Разумеется, скажете вы, в такое легко поверить, ведь он промелькнет так быстро, что к тому моменту как мы засечем, где находится его передняя часть, задняя уже сместится вперед, создавая впечатление более короткого объекта. Нет, нет и нет. Если бы все было так просто!
Если взять ракету с измеренной заранее длинной, в точности равной 1 метру, и выстрелить ей, придав ей скорость близкую к скорости света, чтобы она могла лететь вдоль зафиксированной измерительной ленты, а затем сделать ее мгновенный снимок в полете, вы увидите, что ее длинна будет меньше метра. На сколько меньше — зависит от ее скорости. Чем ближе ее скорость к скорости света, тем сильнее ее сожмет по длине. Я перейду к наиболее подробному объяснению позже, а пока давайте вернемся к шесту и сараю.
Сформулируем нашу задачу иначе: теория относительности говорит нам, что, находясь в сарае и наблюдая за спортсменом, пробегающим вдоль него с шестом в руке, вы увидите, что длина шеста будет меньше длины сарая. Задняя часть шеста скроется в сарае, но передняя покажется с другой стороны несколько позже, и в течение короткого промежутка времени шесть будет целиком находиться внутри сарая.
Но несмотря на всю причудливость, это все еще не парадокс. Теория относительности преподаст нам еще один урок. На самом деле именно благодаря ему она получила свое название: любое движение относительно. Эта идея появилась за много лет до Эйнштейна, и в ней нет ничего по-настоящему странного. Представьте, что вы едете в поезде, а другой пассажир двигается относительно вас в попутном направлении (по коридору поезда). Поскольку вы оба движетесь вместе с поездом, пассажир движется относительно вас на той же скорости, на какой двигался бы, если бы поезд стоял. Но в это самый момент поезд проезжает мимо станции, и наблюдатель на перроне также видит пассажира, идущего внутри вагона. Для него этот пассажир движется быстрее – со скоростью равной сумме его собственной скорости и куда более высокой скорости поезда. Внимание, вопрос: с какой скоростью движется пассажир, идущий по коридору поезда? Со скоростью пешехода относительно вас или с той же скоростью плюс скорость поезда относительно наблюдателя на перроне?
Мы чувствуем себя вполне комфортно, заявляя, что ответ зависит о наблюдателя. Скорость не абсолютна, она зависит от того, с какой скоростью движется человек, измеряющий ее. Аналогично вы можете сказать, что в то время, когда вы находитесь в поезде, сам поезд может считаться неподвижным, а платформа, напротив, движущейся в обратном направлении. Может показаться, что так мы зайдем слишком далеко, потому что более правильно будет сказать, что на самом деле это поезд движется, а не перрон. Но подумайте вот о чем: что если поезд будет ехать с востока на запад с скоростью около 1600 км/час? Представьте, что вы парите в космическом пространстве. Что вы увидите? Вы увидите Землю, вращающуюся на скорости около 1600 км/час в направлении, обратном ходу поезда. Вот чего ей стоит один суточный оборот вокруг своей оси. С вашей точки зрения, поезд едет со скоростью вращения земли под ним, следовательно, не движется. Это все равно, что наблюдать, как кто-то бежит по беговой дорожке. Что вы скажете на этот раз – что поезд едет или земля вращается? Понимаете? Любое движение относительно.
Хорошо, будем считать. Что мне удалось вас убедить. Так что давайте вернемся к шесту и сараю. Хотя бегун с щестом и мчится на нереалистичной скорости, он все еще не может считать себя и свой шест стационарной системой, а сарай – объектом, приближающимся к нему на околосветовой скорости. Теория относительности однозначно говорит нам: с точки зрения бегуна, сарай движется, и он увидит его укороченным по длине. На самом деле он будет значительно короче, чем шест. Потому что для него к тому моменту, как задний конец шеста пройдет через вход сарая, передний давно уже будет снаружи, с другой стороны сарая. В определённый момент времени для него оба конца шеста будут выступать с разных сторон сарая.
В этом и заключается парадокс: с вашей точки зрения, шест короче, чем сарай, и вы, по-видимому, сможете на долю секунды закрыть обе двери сарая, полностью скрыв шест внутри. Но с точки зрения бегуна – шест длиннее сарая, слишком длинный, чтобы поместиться туда. Разумеется, вы и бегу не можете быть одновременно правы. Верный ответ заключается в том, вы в действительности вы оба правы. Это и есть парадокс шеста и сарая.